Davies-Jones Revisited

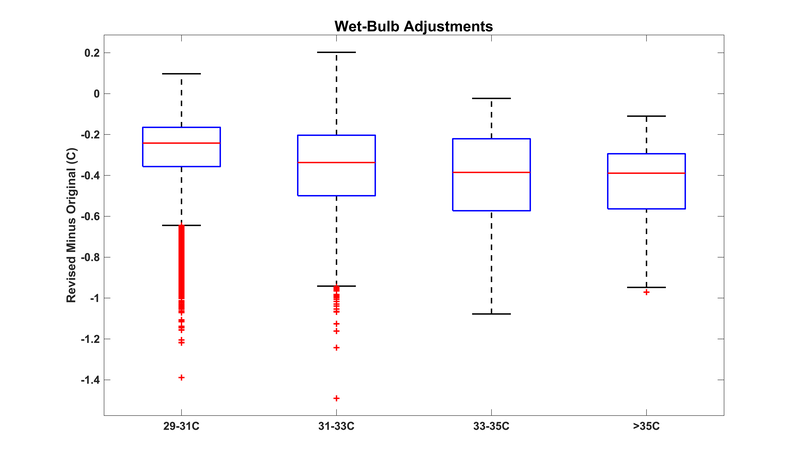
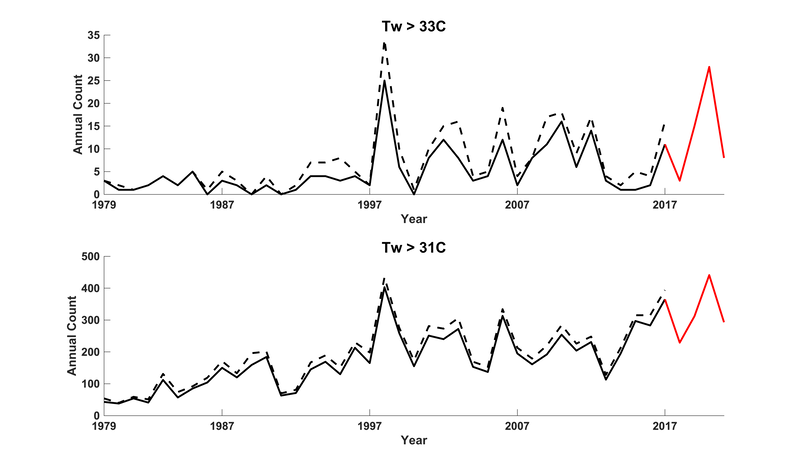
Wet-bulb temperature [Tw] is one of the fundamental metrics governing the workings of the atmosphere, as well as the impacts of weather and climate on humans and other endotherms. For these reasons, and because it captures combinations of temperature and humidity in a globally consistent, human-health-relevant way without relying on difficult-to-measure variables or calibrated indices, much of the foundational research on heat stress has used Tw as the metric of choice. While current understanding has moved beyond a one-to-one relationship between Tw values and physiological stresses, all comparable alternative metrics have similar interpretation caveats. Together with its large and growing base of supporting literature, this means that Tw will likely remain relevant for understanding humid heat stress for quite some time.
 
In an operational sense, Tw's primary drawback is that most of the existing implementations calculate it through a computationally expensive iterative method. This effectively limits large-scale observational or modeling studies to researchers with access to ample processing power, and it hampers efforts to get a better handle on fine-scale spatiotemporal Tw patterns. The most commonly used algorithm is that developed by Davies-Jones (2008), implemented in Fortran 90 by Jonathan Buzan as part of the HumanIndexMod and later translated into MATLAB and Python versions by Bob Kopp and Xian-Xiang Li respectively. Second place in popularity probably goes to the Stull (2011) algorithm, despite its demonstrably larger biases for high heat-stress values, because it is at least an order of magnitude faster than the Davies-Jones codebase.
 
The last year has seen a case of multiple discovery, as two groups have independently pursued approaches to increase the accuracy and efficiency of Tw calculations. [To be precise, this is referring to psychrometric adiabatic Tw, by far the most common Tw variety in climate science.] At the Bureau of Meteorology, Rob Warren and Cass Rogers have developed completely new code that efficiently computes Tw, while at the Jet Propulsion Lab Alex Goodman and I have revised the Buzan/Li implementation to incorporate Numba JIT optimizations. Through our correspondence with each other and with Jonathan Buzan, both groups have detected and removed several longstanding errors, as described further by Rob Warren in this document:
1. incorrect specification of the 'cold' regime
2. incorrect derivative in the main wet-bulb module
3. unnecessary approximations that a) assumed equivalency between specific humidity and mixing ratio and b) assumed relative humidity to be the ratio of actual and saturation mixing ratios (rather than actual and saturation vapor pressures)
 
Code addressing (1) and (3) has been written by Rob Warren, while (2) was addressed several years ago by Qinqin Kong.
 
The Goodman-Raymond Python implementation calculates 10^6 wet-bulb temperatures in about 0.3 seconds on a laptop, or about 50x faster than the Kopp MATLAB implementation, which it should be noted is no longer maintained. The Warren-Rogers implementation (also in Python) is similarly fast.
 
Heritage code has its advantages, of course, but in this case we believe the community can significantly benefit from the adoption of faster and more accurate algorithms. The very success of the Kopp, X. Li, and possible other implementations is what motivates this effort to raise awareness of their need for correction. Code containing all three errors is almost certainly in wide circulation.
 
What implications, then, do these revelations have for the interpretation of existing heat-stress literature? 
 
For the Kopp implementation (the X. Li Python implementation should behave very similarly), when calculating Tw with specific humidity as the input, the errors are rather small for realistic ranges of temperature and humidity (see document linked above for details). Errors 2 and 3 tend to create a negative bias, while error 1 slightly offsets them. With relative humidity as the input, the errors are larger, and error 3 in particular leads to a notable positive bias. Given the air-temperature and relative-humidity ranges associated with global extreme heat stress (see Figure S15 of Raymond et al. 2020), the total Tw error when using uncorrected code for these values is approximately -0.3 to -0.1 C when using specific humidity, or approximately +0.2 to +0.6 C when using relative humidity. A few calculations in very hot and dry climates (temperatures >=45C) have errors up to +1.0C. 
 
Re-evaluating the data underlying Raymond et al. 2020 illustrates and contextualizes these effects more concretely. Depending on the associated relative humidity, an original Tw value of 35.0C becomes 34.0-34.9C with the revisions, scattered around a median correction of -0.4C (Figure 1 below). Around Tw=30C, the correction is closer to -0.25C, and by 20C it is -0.1C. But even restricting our attention to the most extreme observed values, 11 of the 14 Tw>=35C occurrences noted in the paper remain above 35C after correction (Figure 2). The long-term global trends are negligibly affected, as might be expected, and in fact the addition of 2018-21 data arguably makes at least as big of an impact (Figure 3). 

​This critical examination highlights the important point that while accurate code is no doubt important, the results of existing peer-reviewed heat-stress work should be robust to the biasing effects of the recently discovered errors, because a study that sensitive to small differences in Tw should not have been published in the first place. It is also worth emphasizing that this issue should not obscure the existence of other uncertainties attendant in heat-stress studies, many of them less easily quantifiable. For example, the details of the link between Tw and heat stress are subject to conflicting evidence (Baldwin et al. 2023) and to variations across environments and physiologies (Vecellio et al. 2022). Other metrics are difficult to calculate reliably across the globe or have their own idiosyncratic issues. The quantitative conclusions of past heat-stress studies thus might change slightly, but the qualitative ones do not, and certainly the aggregate findings stand up.
 
For future studies using Tw, I would suggest one of several options:
a) An off-the-shelf fresh codebase can be obtained: the Goodman-Raymond implementation is already available on Github, while the Warren-Rogers one (termed NEWT: Non-iterative Evaluation of Wet-bulb Temperature) is currently being written up for publication. With the increase in speed that both offer, there should be no more use case for the fast-but-very-idealized Stull method.
b) Existing code can be modified manually following the description of the errors in the document linked above.
c) If using or evaluating against model output, the HumanIndexMod code remains useful because it reflects how Tw is calculated in CLM5.